The Mathematical Magic of Ellipses

What is an Ellipse?
Imagine a circle that has been stretched out, like a rubber band being pulled from two sides. That stretched circle is called an ellipse. An ellipse looks like an oval—longer in one direction and shorter in the other. You can think of it as a circle’s cousin, because it shares some of the same ideas but also has a few unique features. In the photo above, the ceiling of the Grand Central Train Station in New York City is in the shape of an ellipse. This shape gives the room an amazing property - if two people stand at special places, they can hear each other perfectly, even if they whisper!
These two special places of an ellipse are called “focal points,” often just called foci (pronounced foe-sigh). If you add up the distance from any point on the ellipse to each focus, the total is always the same! This rule is what gives the ellipse its exact shape. A fun way to see this is by tying a string around two pins on a piece of paper and using a pencil to trace the stretched-out path. The shape you draw will be an ellipse! that's the mathematical definition of an ellipse!
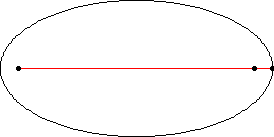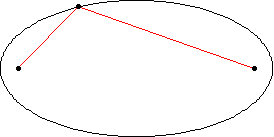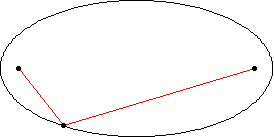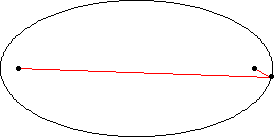
The string method reveals the mathematical beauty of ellipses https://mathworld.wolfram.com/Ellipse.html
Ellipses and Whisper Galleries
In a room that has the shape of an ellipse, when you speak at one focus of the ellipse, sound waves bounce off the curved walls and concentrate at the other focus. This happens because of the reflection property of ellipses - any line from one focus to a point on the ellipse and then to the other focus follows the path that sound or light would take when reflecting off the curve. It's like having a perfectly designed acoustic mirror!
Types of Ellipses
Circle (Special Ellipse)
When both foci are at the same point, you get a perfect circle! A circle is actually just a special type of ellipse where the two focus points have merged into one.
Stretched Ellipse
When the foci are far apart, you get a very stretched, oval shape. The farther apart the foci, the more elongated the ellipse becomes.
Why Are Ellipses Important?
Ellipses appear everywhere in science and nature! Planets orbit the sun in elliptical paths, architects use them to design beautiful domed buildings, and engineers apply elliptical principles in everything from satellite dishes to medical imaging equipment.
Ellipse Quick Facts
- Planetary orbits: All planets travel in elliptical orbits around the sun
- Whispering galleries: Famous examples include St. Paul's Cathedral and the U.S. Capitol
- Medical applications: Kidney stone treatment uses elliptical reflectors to focus sound waves
- Eccentricity: This measures how "stretched" an ellipse is (0 = circle, close to 1 = very stretched)
- Ancient discovery: Greek mathematicians studied ellipses over 2000 years ago
- Pool tables: Elliptical pool tables create fascinating ball trajectories
See Ellipses in Action
Watch this fascinating demonstration of how elliptical shapes are used in a wide variety of practical applications!
Ellipses in Thunder Cloud Summer
In our story, Kenilsworth's Hall of Whispers demonstrates this mathematical principle perfectly:
- Focal points: The golden stars on the floor mark the two foci of the ellipse
- Perfect acoustics: Sound from one star focuses perfectly at the other
- Ancient engineering: Real buildings like this exist around the world
- Mathematical precision: The dome's shape follows exact elliptical geometry
Try it Yourself!
Make Your Own Ellipse
Materials:
- Large piece of paper or cardboard
- Two thumbtacks or pushpins
- String (about 12 inches long)
- Pencil
- Ruler
Instructions:
- Push the two thumbtacks into your paper, about 4 inches apart
- Tie the string into a loop around both thumbtacks
- Put your pencil inside the string loop and pull it tight
- Keeping the string taut, move the pencil around to draw your ellipse
- Try moving the thumbtacks closer or farther apart and see how your ellipse changes!
What This Shows:
The string ensures that the distance from your pencil to both thumbtacks always adds up to the same total. This is the mathematical definition of an ellipse! Try measuring the distances and you'll see this relationship in action.
Mathematical Challenge: Can you figure out the relationship between the string length and the size of your ellipse? What happens when the thumbtacks are very close together versus far apart?
Want to Learn More?
- Wolfram MathWorld - Ellipses - Comprehensive mathematical properties
- CK-12 Foundation - Equation of an Ellipse
- Kiddle - Ellipse Facts for Kids